数据滤波是去除噪声还原真实数据kalman和传统滤波区别的一种数据处理技术, Kalman滤波在测量方差已知kalman和传统滤波区别的情况下能够从一系列存在测量噪声的数据中,估计动态系统的状态 由于, 它便于计算机编程实现, 并能够对现场采集的数据进行实时的更新和处理, Kalman滤波是目前应用最为广泛的滤波方法, 在通信, 导航, 制导与控制等多领域得到;滤波过程涉及两种误差估计误差和测量误差当估计误差远大于测量误差时,滤波器会更信任当前的测量值,反之则更依赖于先前的估计值Kalman增益是一个关键参数,它决定kalman和传统滤波区别了测量值和估计值在更新过程中的权重协方差矩阵的作用协方差矩阵在卡尔曼滤波中至关重要,它反映了变量间的关联性通过矩阵运算。
CPUKF和K的区别 滤波算法是信号处理领域中常用的技术,用于从带有噪声的测量值中提取有用信息本文将重点比较两种优化滤波算法卡尔曼滤波K和扩展卡尔曼滤波CPUKF之间的区别,并探讨它们在滤波应用中的优势CPUKF与K滤波算法的基本原理比较1CPUKF算法的基本原理及特点详解CPUKF算法在;ERKF是Extended Kalman Filter的缩写,是一种非线性滤波器它是从卡尔曼滤波器Kalman Filter发展而来的,解决了非线性过程建模的问题ERKF与传统的线性卡尔曼滤波器相比,适用范围更广,精度更高,能够适应更复杂的实际问题ERKF在众多领域都有广泛的应用在导弹制导航空航天自动控制机器人。
1 定义与起源 定义卡尔曼滤波算法通过结合系统动态模型的先验知识和当前的观测数据,对系统的状态进行最优估计起源该算法由鲁道夫·卡尔曼在1960年提出,是现代控制理论中的重要组成部分2 核心思想 系统模型包括状态转移方程和观测方程状态转移方程描述系统状态随时间的变化,而观测方程描述如何。
kalman滤波算法是算什么的
卡尔曼滤波器是一种状态估计器,它通过融合传感器和信息来提升系统精度在观测系统状态时,通常有两种方法一种是通过状态转移方程,结合上一时刻的状态预测下一时刻的状态另一种是借助辅助系统如量测系统的测量来获取系统状态这两种方法都存在不确定性,卡尔曼滤波通过加权平均这两种方法,使估计。
无迹卡尔曼滤波Unscented Kalman Filter,UKF,是一种专为非线性动力学和测量模型设计的状态估计技术相较于传统的卡尔曼滤波,它在处理非线性系统时更为适用,能有效降低估计误差UKF采用无迹变换,将非线性系统的高斯分布映射到线性空间,进而运用卡尔曼滤波原理进行预测和滤波UKF的关键在于无迹样。
卡尔曼滤波不要求信号和噪声都是平稳过程的假设条件对于每个时刻的系统扰动和观测误差即噪声,只要对它们的统计性质作某些适当的假定,通过对含有噪声的观测信号进行处理,就能在平均的意义上,求得误差为最小的真实信号的估计值因此,自从卡尔曼滤波理论问世以来,在通信系统电力系统航空航天。
但是由于GPS定位包含许多误差源,尤其是测量随机误差和卫星的几何位置误差,使定位精度受到影响利用传统的方法很难消除而GPS动态滤波是消除GPS定位随机误差的重要方法,即利用特定的滤波方法消除各种随机误差,从而提高GPS导航定位精度 经典的最优滤波包括Wiener滤波和Kalman滤波由于Wiener滤波采用频域法。
卡尔曼kalman滤波卡尔曼滤波是一种高效率的递归滤波器自回归滤波器, 它能够从一系列的不完全包含噪声的测量英文measurement中,估计动态系统的状态应用实例卡尔曼滤波的一个典型实例是从一组有限的,对物体位置的,包含噪声的观察序列预测出物体的坐标位置及速度 在很多工程应用雷达, 计算机。
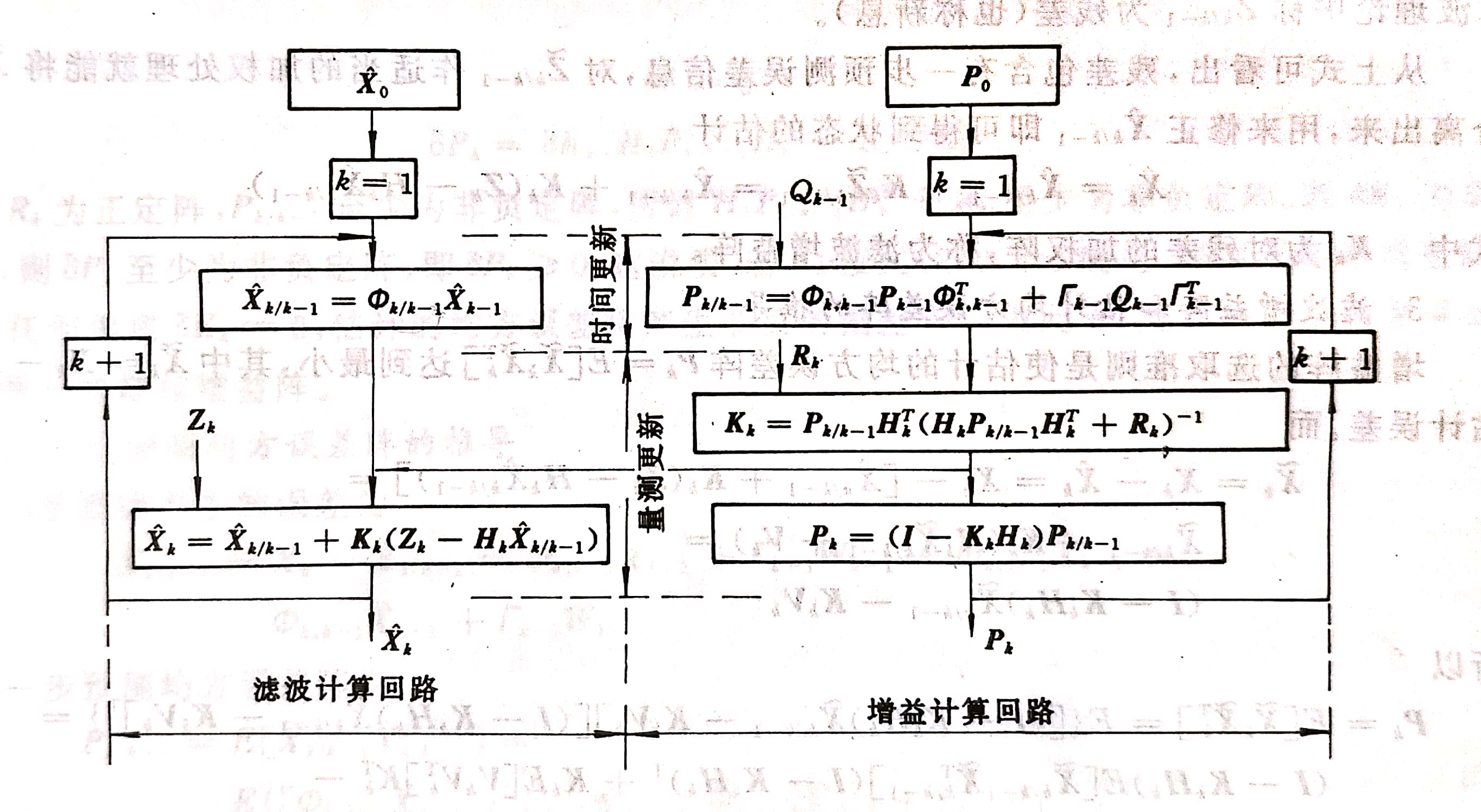
kalman滤波理论及其在导航系统中的应用
滤波是信号处理中的关键环节,目的在于从混杂着噪声的信号中提取出有用的信息在卡尔曼滤波出现前,已有最小二乘法与维纳滤波等理论来处理观测数据与平稳随机过程,但它们存在功能不足或条件苛刻的局限性卡尔曼滤波的提出,旨在克服这些局限,成为滤波技术的重大革新相较于维纳滤波,卡尔曼滤波拥有以下。
随着传感技术机器人自动驾驶以及航空航天等技术的不断发展,对控制系统的精度及稳定性的要求也越来越高卡尔曼滤波作为一种状态最优估计的方法,其应用也越来越普遍,如在无人机机器人等领域均得到了广泛应用对于卡尔曼滤波的理解,用过的都知道“黄金五条”公式,且通过“预测”与“更新”两。
与卡尔曼滤波Kalman Filter相比较 粒子滤波PF Particle Filter的思想基于蒙特卡洛方法Monte Carlo methods,它是利用粒子集来表示概率,可以用在任何形式的状态空间模型上其核心思想是通过从后验概率中抽取的随机状态粒子来表达其分布,是一种顺序重要性采样法Sequential Importance Sampling简。
总结 我们可以用这些公式对任何线性系统建立精确的模型,对于非线性系统来说,我们使用扩展卡尔曼滤波,区别在于EKF多了一个把预测和测量部分进行线性化的过程参考文章 akalmanfilterworksinpictures detail。
两种滤波方法之间的区别主要体现在以下两个方面首先,卡尔曼滤波适用于处理非平稳过程,而维纳滤波则不适用于此其次,维纳滤波能够处理无限维系统,尽管这在谱分解方面较为复杂,而卡尔曼滤波对无限维系统则无能为力卡尔曼滤波与维纳滤波在实际应用中的选择依赖于具体问题的特性和需求卡尔曼滤波因其。
卡尔曼滤波Kalman Filter和IIR滤波Infinite Impulse Response Filter是两种不同的滤波方法1 工作原理 卡尔曼滤波是一种最优估计滤波方法,通过对系统状态的动态建模和测量数据的融合来估计未知量它利用状态方程和观测方程,通过递归迭代的方式来估计真实状态,并通过方差最小化准则来估计状。
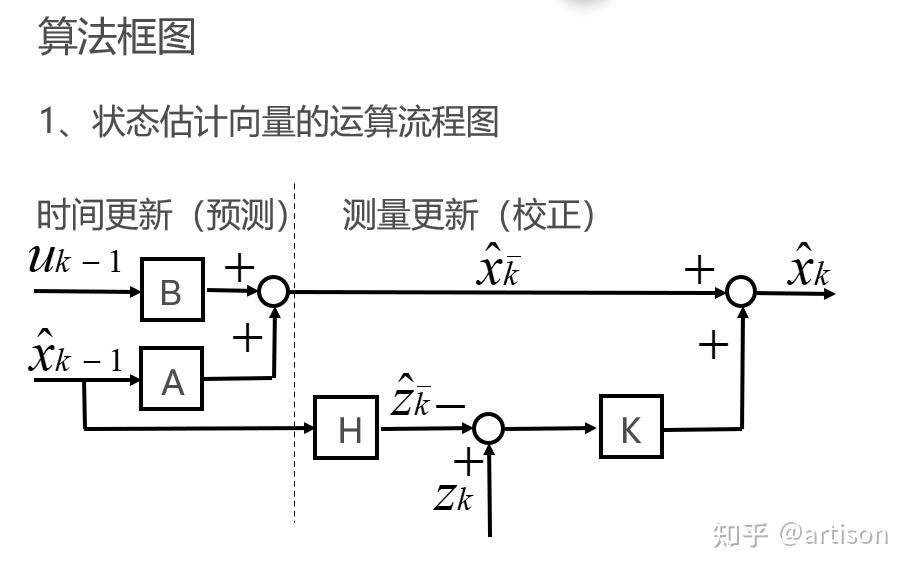
卡尔曼滤波是一种递归算法,它在时刻k对z进行测量时,通过公式公式更新估计值随着观测数据增多,测量值的影响力逐渐减弱,而依赖于先前估计值的系数公式则逐渐增强核心公式是公式,描述了当前估计值如何结合新的观测值和上一时刻的估计滤波过程涉及两种误差估计误差公式和测量误差公式。
